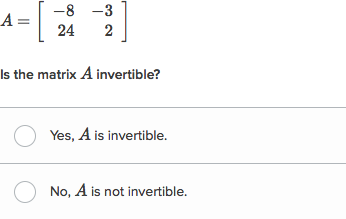Fine Beautiful Tips About How To Check If A Matrix Is Invertible

But p+q is just as noninverable as before.

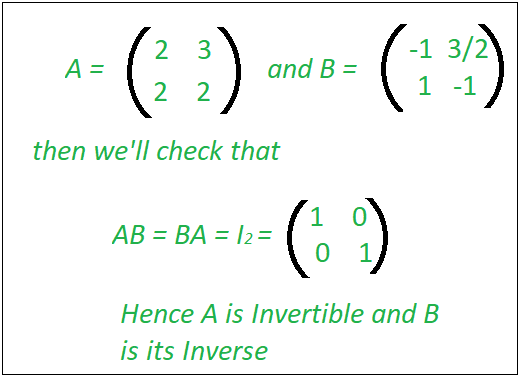
How to check if a matrix is invertible. There are many way to check if a is invertible or not. Then if you are left with a matrix with all zeros in a row, your matrix is not invertible. 3)the system ax=0 has trivial solution.

The invertible matrix determinant is the inverse of the determinant: A matrix is invertible if and only if its determinant is not zero. How do you check if a matrix is invertible?

Let us check the proof of the above statement. M − 1 = a d j ( m) | m |. If the determinant of the matrix a were undefined.

To calculate the inverse of a matrix we divide the. Meanwhile cond does change a. Using abs (det (m)) > threshold as a way of determining if a matrix is invertible is a very bad idea.

Any square matrix a over a field r is. The invertible matrix theorem is a theorem in linear algebra which offers a list of equivalent conditions for an n×n square matrix a to have an inverse. So if the determinant comes out to be zero, the matrix is not.

Take a matrix such as a and find out its. If the matrix is singular then it is not invertible and if it is non−singular then it is invertible. 1)det (a) unequal to zero.